Compass

Compass is a toy language for compass & straightedge constructions, with easy syntax and visualization.

Example

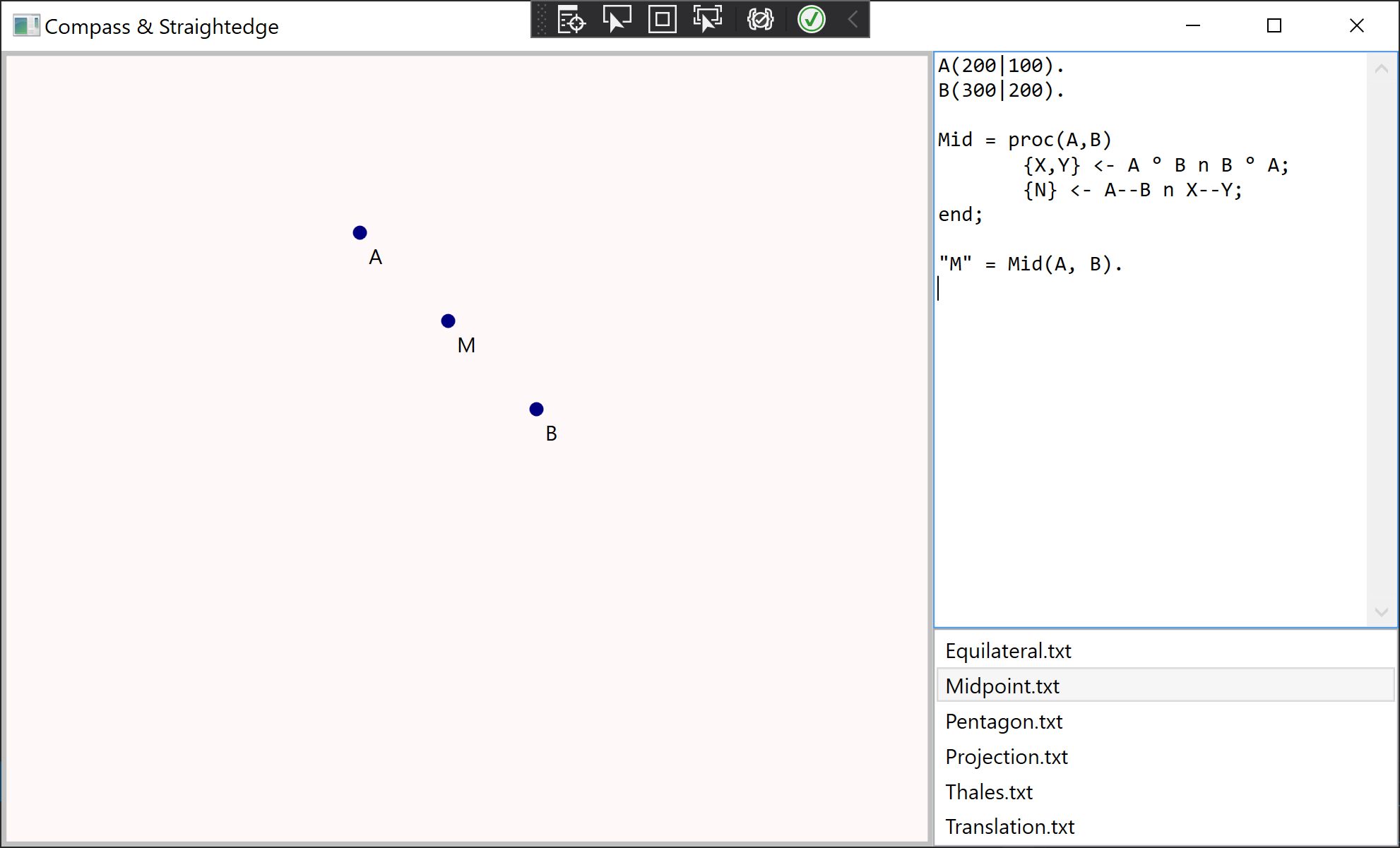
A(1|1), B(2|4). // define and name some points
    
C1 = A°B; // circle around A through B
C2 = B°A; // circle around B through A

{X1, X2} <- C1 n C2; // compute intersection of circles
{"M"}    <- (X1-X2) n (C1-C2) // compute intersection of lines, giving the midpoint of A and B

Language

A Compass program consists of a sequence of statements, separated by commas, semicola or periods. A statement followed by ; is silenced, meaning its result will not be drawn. Otherwise, its result will be displayed.

Statements

Statements have the following forms

1. Named point definitions

   A(20|50)
   

   defines a named pointed "A" and assigns it to the variable A. A named point will, when drawn, have its name displayed alongside it.

2. Assignments

   X = <expr>
   

   Assigns to the variable X the result of expression <expr>. Variables must begin with uppercase letters. The overall assignment evaluates to the variable X

3. Pick assignments

   {X1, ..., XN} = <expr>
   

   If <expr> evaluates to a set, the pick assignment statement tries to pick N distinct elements from that set (in any order) and assigns them to variables X1 to XN. The overall assignment evaluates to the last variable assigned. One can (experimentally) pick from infinite sets such as circles and lines; the points thus obtained are random

   {A,B,C} <- M°P // pick three random points from a circle

4. Bonus (Named assignments): If we put quotation marks around a variable in an assignment, if it is assigned a point, the point is upgraded to a named point as in

   {"X"} <- Line1 n Line2 
   

   This, together with Named point definitions, is the only way of creating named points.

Expressions

Expressions have the following forms

Lines and segments

A-B  // line segment AB
A->B // ray (half-line) from A through B
A--B // infinite line through A, B 

Circles

M°P   // circle around M through P
M o P // alternative syntax

Set operations

A n B // intersection
A u B // union
A \ B // subtraction

Procedures

// returns the midpoint between points A, B
Midpoint = proc(A,B)
  {X,Y} <- (A°B) n (B°A)
  {M} <- (X--Y) n (A--B) 
end

Procedure calls

Midpoint(A,B)

Datatypes

The datatypes currently supported in Compass are: Point, NamedPoint, Circle, Line, Ray, Segment, PointSet, Lambda

More examples

A list of examples is found in the Samples folder. The Compass application includes a sample browser.

Construction of a regular pentagon

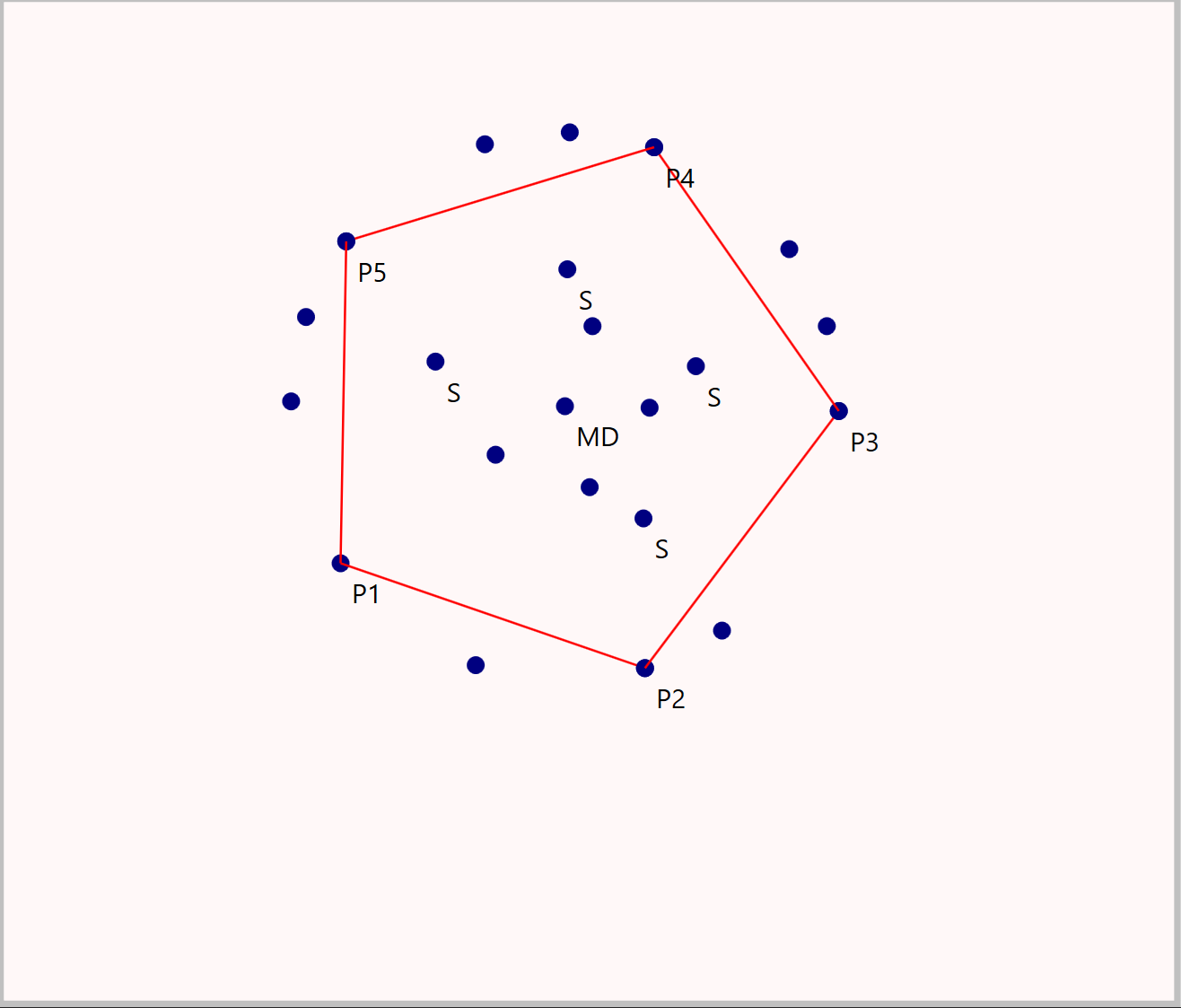
// Construction of a regular pentagon

MD(250|180), P1(150|250). 

// midpoint between two points
Mid = proc(A,B)
	{X,Y} <- A°B n B°A;
	{R} <- (X--Y) n (A--B);
end;

// angle bisector
HalfAngle = proc(A,B,C)
	{D} <- (A°B) n (A->C);
	X = Mid(B,D);
	A->X;
end;

// parallel line to A--B through P
Parallel = proc(P,A,B)
	{X} <- P°A n A--B;
	{Y} <- X°P n A--B;
	{R} <- Y°X n P°A;
	P--R;
end;

// make a 72° move from M-P
Penta = proc(M,P)
	{Q} <- ((P--M) n M°P) \ {P}.
	{X,Y} <- P°Q n Q°P; 
	{R} <- (X--Y) n M°P.
	"S" = Mid(R,M).
	{H} <- HalfAngle(S,M,P) n M--P.
	{P2} <- Parallel(H,M,R) n M°P.
	P-P2, P2;
end;

"P2" = Penta(MD,P1).
"P3" = Penta(MD,P2).
"P4" = Penta(MD,P3).
"P5" = Penta(MD,P4).
P5-P1.

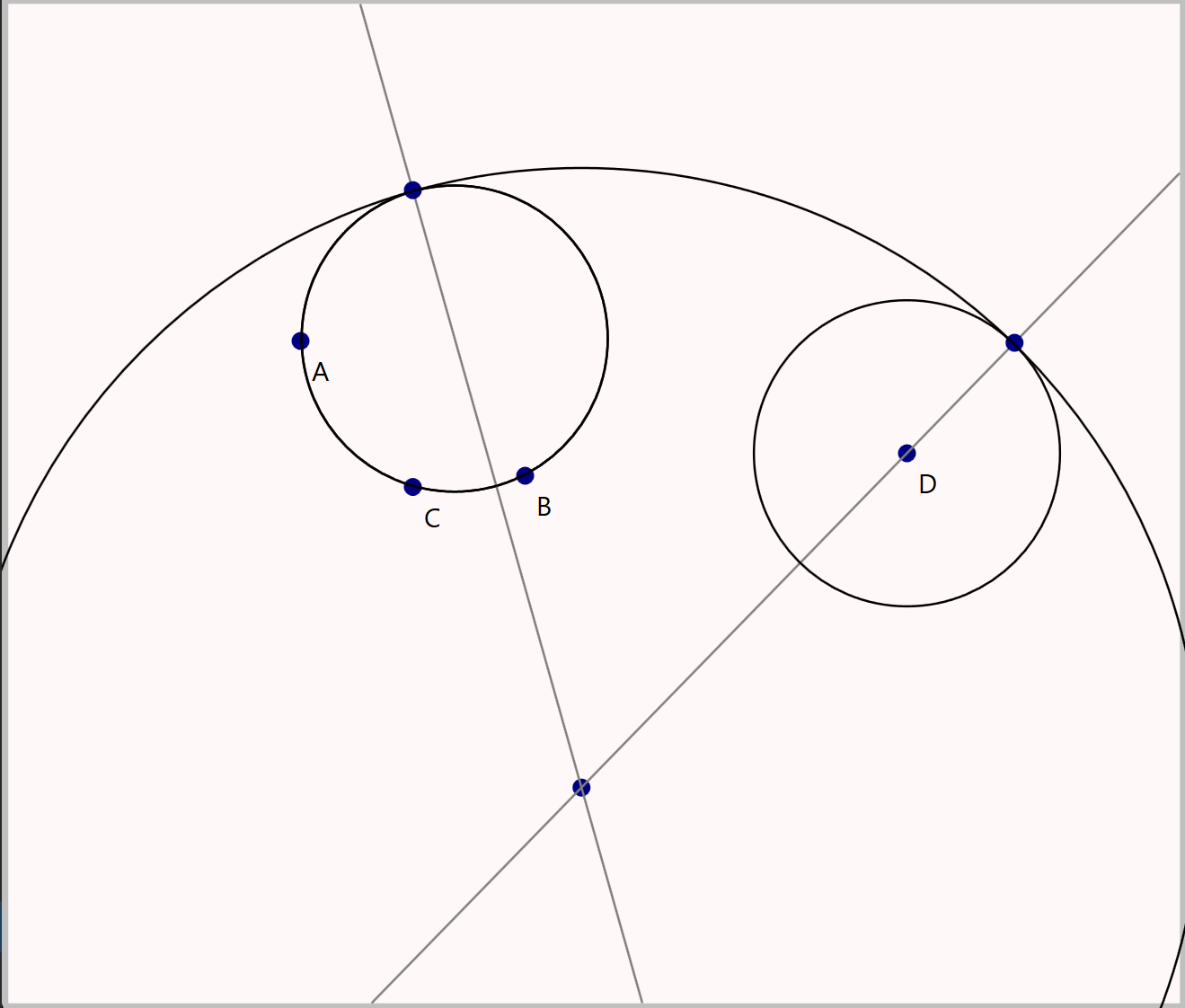
Translation of a circle

A(130|150), B(230|210), C(180|215), D(400|200).

Mid = proc(A,B)
    {X,Y} <- A°B n B°A;
    {M} <- (X--Y) n (A--B);
end;

Circle = proc(A,B,C)
	{X,X'} <- A°B n B°A;
	{Y,Y'} <- B°C n C°B;
	{M}    <- (X--X') n (Y--Y');
end;

Center = proc(C) {A,B,C} <- C; Circle(A,B,C); end;

CEQ = proc(A,B,C)
	{D} <- A°B n B°A,
        D--B, B°C,
	{E} <- (D--B) n B°C,
        D--A, D°E,
	{F} <- (D--A) n D°E.
	A°F;
end;

Move = proc(C,A) 
	M = Center(C);
	{B} <- C;
	CEQ(A,M,B);
end;

K = (Circle(A,B,C))°A.
Move(K,D).

Technical note

This is a very old hobby project. Its original goal was to test the interaction of F# with other .NET languages, parser combinators, definitional interpreters and the Visitor pattern, as well as doing some fun geometry.