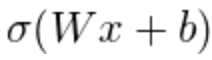Activation Function
- Perceptron의 출력값을 변형시키는 역할/입력값의 총합을 출력으로 변환. Perceptron의 출력을 비선형으로 변환하기 위해 사용한다.
- input값 x와 weight W를 곱하고 bias b를 더한뒤 씌워주는 활성 함수.
-
- 여러 층으로 된 모델을 하나의 층만으로도 나타낼 수 있어서 레이어를 여러 층 쌓은 것을 무용지물로 만든다.
- Activation Function이 선형 함수이면, 레이어를 여러 층 쌓은 것을 행렬의 곱으로 나타낼 수 있다. 행렬을 곱한 값은 하나의 행렬로 나타낼 수 있다. 그러므로 레이어가 여러 층 쌓여 있더라도, 하나의 레이어로 나타낼 수 있는 것이다.
- ex) h(x) = cx를 활성화 함수로 3layer network를 만들면 y(x) = ccc*x = c^3(x) 가 되므로 또 하나의 y(x) = ax 꼴이 되어버린다.
- vanishing gradient
- back propagation(틀린정도를 미분한 것을 전달)에서 레이어가 깊을 수록 업데이트가 사라지면서, underfitting 발생
- 퍼셉트론의 활성화 함수.
- 퍼셉트론에서 입력 각각을 각각의 weight에 곱한 뒤, bias를 더한 값이 0 이하이면 0, 0 초과이면 1을 출력한다.
- 1단계: 입력 각각을 각각의 weight에 곱한 뒤 bias를 더한다.
- 2단계: 1단계의 값이 0 이하이면 0, 0 초과이면 1을 출력한다. (활성화 함수 적용 단계)
- 값 범위: 0 이상 1 이하
- 0에서 1 사이의 값을 갖는 함수로 0 근처에선 기울기가 크나 0에서 멀어질수록 기울기가 작아진다. 그래서 모델에 Layer가 많을 때 이 활성화 함수를 사용하면 학습이 잘 안 된다.
- 그럼에도 불구하고 비선형 함수로서 잘 쓰였던 이유
- 미분이 편리 : 자기 자신으로 미분된다
- 확률 값을 리턴
- 0 이하는 0, 0 초과는 입력값을 그대로 내놓는 함수.
- 비선형 함수.
- 입력값이 0 이하면 모든 출력이 0이 되는 단점이 있다.
- numpy로는
np.maximum(0, x)으로 구현할 수 있다.- x는 배열이며, 배열 내의 값이 0 이상이면 그 값을, 0 미만이면 0으로 채우는 함수
- 각 입력값을 정규화해서 최대가 1인 확률값을 만드는 활성화 함수.
- 분류(Classification)를 한다면 출력 Layer를 Softmax로 하면 된다.
- 숫자가 매우 크면 overflow가 발생할 수 있다.
- 로그 법칙에 의하여 softmax를 구할때 입력값, 입력값의 합 각각에 같은 수를 더하거나 빼어도 값은 동일하다.
- 보통 입력값의 최댓값을 뺀다.
- 0 이상이면 입력값을 그대로, 0 보다 작으면 매우 작은 값(예: 0.01 등)을 곱해서 출력하는 함수. ReLU에서 발생하는 dying ReLU를 보완하기 위한 함수이다. 여기서 dying ReLU이란 ReLU에서 입력이 0 이하라면 전부 0으로 출력되어서 일부 뉴런이 전혀 출력되지 않는 현상이다.
- 0 이상이면 입력값을 그대로, 0 보다 작음면 ax를 출력한다.
- 0 이상이면 입력값을 그대로, 0 보다 작으면 a(e^x-1)를 출력한다.
- ReLU
- 무난한 선택. 특히 계층이 깊을 때.
- 비선형 함수이기 때문에 자주 쓰인다.
- Sigmoid
- 출력값이 확률값인 경우: sigmoid 함수의 범위가 0과 1 사이에 있기 때문.
- 이진 분류 (0/1으로 분류)
- Softmax
- Classification 문제인 경우: softmax 함수의 출력값의 합이 1이기 때문